Towers of Hanoi and Sierpinskis Triangle

The Towers of Hanoi
The towers of hanoi puzzle has existed since 1883, For those unfamiliar with the puzzle it is a puzzle involving disks of increasing radius stacked on pegs. The aim of the game is to move the disks from the first peg to the last, obeying the following rules
-
Only one disk can be moved at a time.
-
Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
-
No disk may be placed on top of a smaller disk.
The most efficient solution to this problem requires \(2^n - 1\) moves to solve where n is the number of disks

Augmented Towers
There is a slight variant of the Towers of Hanoi puzzle that edits the 2nd rule. Now you may only move a disk from a peg to a directly adjacent peg, so moves between pegs 1 and 2, and between 2 and 3 are allowed, but no longer between 1 and 3.
This new variant is best solved in \(3^n - 1 moves\). However, there are only 3^n possible arrangments for the Puzzle to be in, therefore the solution to the augmented puzzle must pass through all possible arrangments of the puzzle, without ever going back.
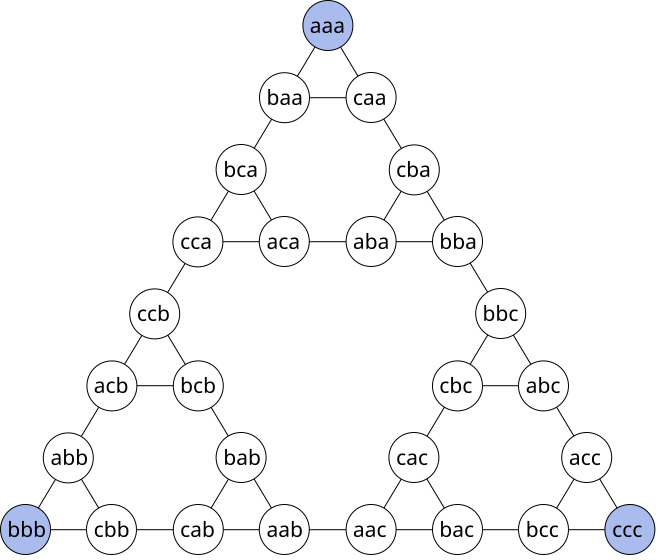
State Space Graph
The state space of the Hanoi Problem can be constructed from small self similar triangles, first create a vertex for each of the three possible positions of the largest disk, these vertices form a connected triangle.
Next break each vertex up into three more vertices, where each vertex represents the different position of the 2nd biggest disk, given the fixed position of the largest.
Continue this process until you reach the smallest vertex, and then connect all states together that are reachable by moving one disk. Its clear to see what you’ve constructed is a Sierpinskis Triangle
The Grand Tour
Now we know we have a method of traversing every state of the Hanoi problem, and we know that the state space can be represented by a Sierpinskis triangle.
Therefore we can write a method to solve the Towers of Hanoi with n disks, and adapt it to draw the nth iteration of Sierpinskis triangle.
I wrote a simple recursive solution to solve the augmented towers problem and then added in some calls to the python “turtle” graphics library to draw the curve
3 disks

4 disks

7 disks

8 disks
