Graphs, Topology and the Game of Life

Game of Life

Conway’s Game of Life is the most famous example of a “Cellular Automaton”.

We consider a whole infinite 2d grid of cells, each cell is either dead or alive, and we allow the cells to evolve over time. The rules by which cells evolve are decided by their neighbours.

1. Any live cell with 2 or 3 neighbours survives.
2. Any dead cell with 3 live neighbours becomes alive (is born).
3. All other live cells die, and all other dead cells stay dead.

These simple rules give rise to very complex behaviour, such as this repeating pattern known as “Gosper’s Glider gun”:

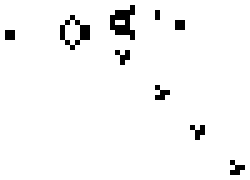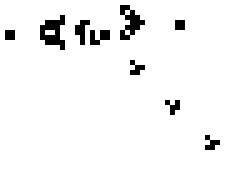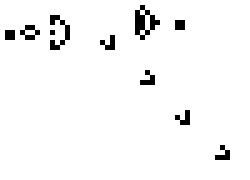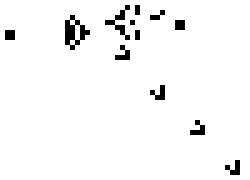
Cellular automata take this idea and generalise it, adding more states than just “dead” and “alive”, and looking at neighbours in 1 dimension or 3 dimensions instead of just 2. Cellular automata are not just visually pretty, they’re also powerful, they can compute any programs that any computer can, you can even simulate Conway’s game of life in Conway’s game of life. They don’t even need to be 2 dimensional, shockingly there exists simple 1 dimensional cellular automata are theoretically able to compute anything that any supercomputer could.

But what if we’re sick of just 2 dimensions, 3 dimensions or even 4 dimensions? What if we want to compute in arbitrary dimensions, or compute in pacman’s wrap-around world? We need to think about what we mean when we say “neighbours”.

Graphs

Graph theory is the first tool that jumps to mind when I think about neighbours. Graphs are defined as a set of nodes, and a set of relationships, the relationships tell you what nodes are neighbours of what other nodes. We usually visualise graphs as circles and lines, the circles are the nodes, and the lines connect the neighbours.

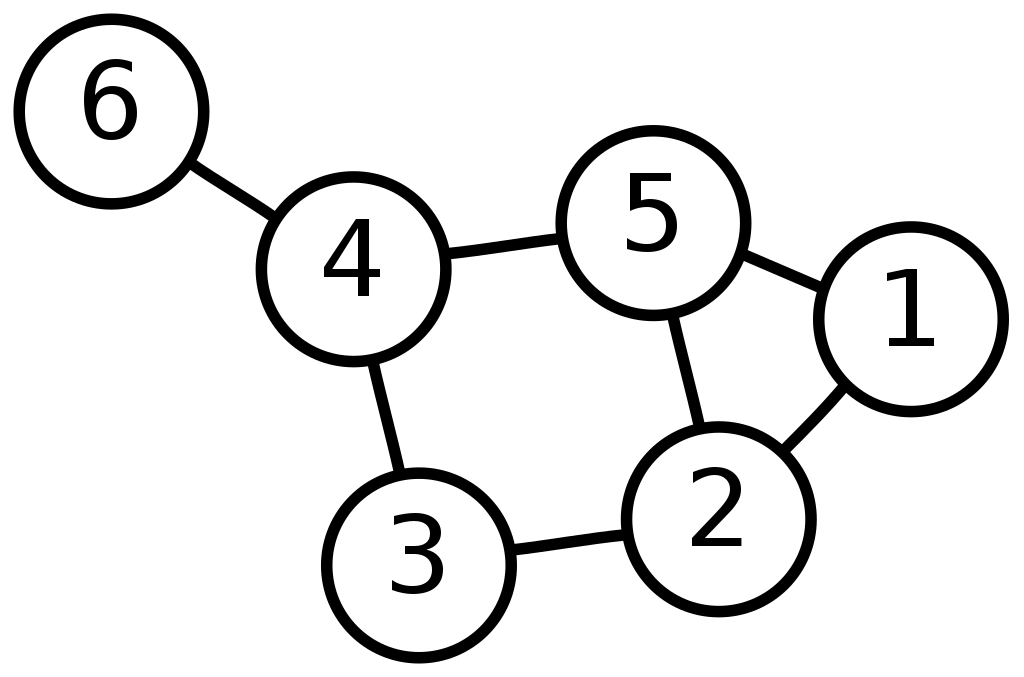
In Conway’s game of life, neighbours of a cell are all the 8 surrounding cells, we can draw this as a graph like this:

Each cell has 8 lines coming from it, connecting to its 8 surrounding neighbours.

Now that we’ve taken away the grid, we can start changing things up, we can start adding lines and removing lines all we want. We could use this to represent any simple structure we could think of, for example, we could consider a 2D grid, but only connect cells that a chess knight can jump between; We get this much more complex looking graph:

Every cell still has eight neighbours, so lets run a simulation with the same rules as the game of life:

(You can play with this simulation in Setanta here)

You could imagine how this idea could be used to consider cellular automata in all sorts of wild and wonderful situations. You could have a cellular automata with the structure of the road network of your respective country, or construct a graph of a population, with edges for people who regularly come into contact, and use it to do simple disease modelling, the list goes on.

There is another area of mathematics that’s all about neighbourhoods, and in fact is closely related to graph theory.

Topology

Topology is often called rubber sheet geometry, most people understand it as the doughnuts = coffee cup kinda maths, the study of what shapes are functionally equivalent if you’re allowed to stretch’em and squish’em.

At it’s core though, topology is all about neighbourhoods. It’s all about what points are in some way adjacent to other points. When you think about your neighbourhood, you might think of your immediate adjacent neighbours, or maybe your whole street or estate. All of these would be considered neighborhoods from topology’s perspective. When we say neighborhood we effectively mean a set of points that are in some way related to each other, our topology defines exactly what way they’re related.

Formally speaking a topology \(T\) on some set \(X\) is a collection of subsets of \(X\) satisfying some simple conditions. The elements of \(T\) are our neighbourhoods. These conditions guarantee that elements of \(T\) behave like neighbourhoods around points.

1. \(X\) and the empty set are both neighbourhoods.
2. A union of any amount of neighbourhoods is still a neighbourhood.
3. Any intersection of some finite amount of neighbourhoods is still a neighbourhood.

For example, on the 2d-plane, we could call any circle around a point a neighbourhood of that point.

The way we describe the neighbourhoods tells us then how we can stretch and squish our shapes, we can do whatever we want without ripping or tearing up our neighbourhoods (roughly).

So what can topology tell us about cellular automata? One of the first thing that we can look at is what structures can we represent with real objects? Which cellular automata can be physically put into 2D space, or 3D space?

Pacman’s game

The world of pacman is a world where going out the left side brings us back to the right side, and going out on the top brings us back at the bottom. We could represent this with a graph by connecting the top and bottom vertices, and the left and right vertices, then connect the others in the usual fashion.

Using the game of life glider we can watch this wrap around behaviour:

Can we represent this in a real physical space? This is a well explored topic in topology, and the answer is yes. Imagine taking a piece of paper, we want to join the left and right sides, and the top and bottom. First we wrap the piece of paper into a cylinder to join the left and right sides, then we can twist the piece of paper around to join the top and the bottom; What we’re left with is a doughnut (a torus).

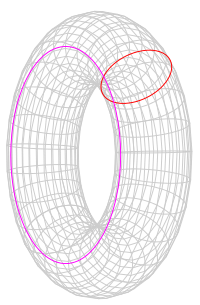
This means we can embed our pacman world game of life simulation into the real world. You can see this in action here or here.

Side note

You might be familiar with the mathematician John Nash, subject of the book and movie “A Beautiful Mind”. He’s most famous for winning the Nobel prize for Economics, but some of his breakthrough work in topology gives rise to a fascinating way of embedding the torus shown above in 3d space. The details are outside the scope of this post. I just think the picture is fascinating.

Topology vs Graphs?

Both topology and graph theory deal with neighbourhoods, so what’s the difference? What can topology give us that graph theory can’t.

The key detail here is that, unlike in graph theory, neighbourhoods in topology points (usually) have infinite neighbourhoods, that range from infinitesimally small to infinitely large, and vary continuously between. Graph theory however is stuck with just the one definition of neighbourhood.

Breaking free from this discrete viewpoint, we can define so called “continuous spatial automata”, which are cellular automata that aren’t strictly limited to some discrete set of locations, instead we can have cells at infinite points, imagine that each real number on the number line is a distinct cell. The state of these cells can then be varied over time just like with our original cellular automata. This can be used to simulate much more complex systems, such as the spread of heat over a surface.